Electrochemical and Biological Membranes

Introduction. Mass and charge transport processes play an important role in many areas of science. In the field of ion-selective electrodes transport of ions determines the generation of electrochemical signals. The membrane processes involving charge transport are of vital importance in cell biology since they support homeostasis of living organisms.

Mathematical model. Model based on mass balance and Poisson equations together with constitutive Nernst–Planck flux formula was developed. The model describes the processes of electrodiffusion in systems composed of many layers (Fig.1)  such as, for example, internal solution/ion selective membrane/diffusion layer/sample solution. It takes into account reaction terms in mass balance equation, charge conservation equation and kinetics of ion transport across the boundaries in the form of Chang-Jaffé boundary conditions. It is worth noting that the model does not assume commonly used simplifications such as electro-neutrality or constancy of the electric field.

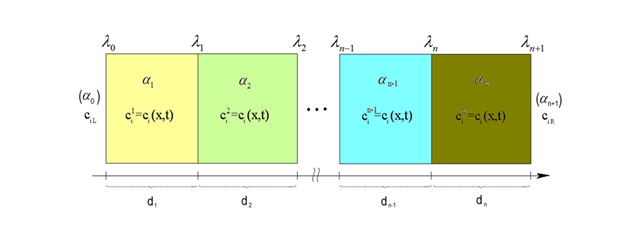
Fig. 1. Schematic representation of the multi-later space region for model of electrodiffusion [2].

Numerical method. Numerical solution using method of lines developed. The established cooperation with the Faculty of Applied Mathematics, AGH-UST allowed to proove the existence and uniqueness of electrodiffusion problem in multicomponent systems for time-dependent (non-stationary) equations and generalized Chang-Jaffé boundary conditions.

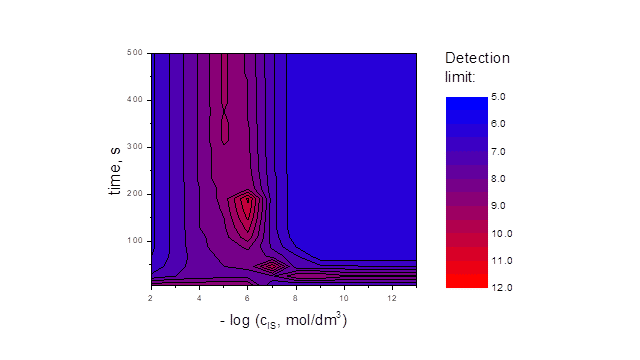
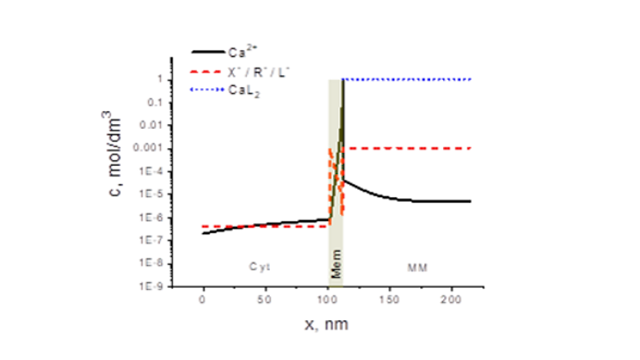
Applications. Developed model was applied to model transient behavior of various electrochemical processes in ion-selective membranes. Multi-layers and reactions are formally admitted making possible modeling of the influence of ion diffusivities, membrane thickness, permittivity, rate constants on the potential of membranes. The inverse problem applied to electrodiffusion problem allowed optimizing sensor properties and measurement environment. Conditions under which experimentally measured selectivity coefficients are true (unbiased), ion interference on ion-sensor responses and the detection limit optimization were performed. Modeling of ion transport in biological membranes was demonstrated. The calcium set-point, i.e., concentration of calcium in cytosis below which calcium stops entering into a mitochondrion was calculated.

Fig.2. Time-concentration-detection limit map obtained using electrodiffusion model [8].
Fig. 3. Calcium concentration profiles for two different values of calcium ions concentration in cytosol [7].

Cooperation. Projects realized in cooperation with the Åbo Akademi University, Turku, Finland and Warsaw University of Life Sciences – SGGW and the Faculty of Applied Mathematics AGH-UST.

Research papers:

  1. R. Filipek, K. Szyszkiewicz-Warzecha, B. Bożek, M. Danielewski, A. Lewenstam, „Diffusion transport in electrochemical systems: a new approach to determining of the membrane potential at steady state”, Defect and Diffusion Forum, 283–286, (2009), 487–494.
  2. J. J. Jasielec, R. Filipek, K. Szyszkiewicz, J. Fausek, M. Danielewski, A. Lewenstam, „Computer simulations of electrodiffusion problems based on Nernst-Planck and Poisson equations”, Computational Materials Science, 63, (2012),75–90.
  3. J. Fausek, K. Szyszkiewicz, R. Filipek, “Numerical Aspects of Electrodiffusion Problem Based on Nernst-Planck and Poisson Equations”, Defect and Diffusion Forum, 323-325, (2012), 81–86.
  4. J.J. Jasielec, T. Sokalski, R. Filipek, A. Lewenstam, „Comparison of different approaches to the description of the detection limit of ion-selective electrodes”, Electrochimica Acta, 55, (2010), 6836–6848.
  5. J.J. Jasielec, T. Sokalski, R. Filipek, A. Lewenstam, „Neutral-carrier ion-selective electrodes assessed by Modelowanie transport the Nernst-Planck-Poisson model”, Analytical Chemistry, 87, (2015), 8665–8672.
  6. P. Lingenfelter, B. Bartoszewicz, J. Migdalski, T. Sokalski, M. M. Bućko, R. Filipek, A. Lewenstam, “Reference Electrodes with Polymer-Based Membranes—Comprehensive Performance Characteristics”, Membranes, 9, (2019), 161–183.
  7. J.J. Jasielec, R. Filipek, K. Szyszkiewicz, T. Sokalski, A. Lewenstam, „Continuous Modelling of Calcium Transport through Biological Membranes”, Journal of Materials Engineering and Performance, 25, (2016), 3285–3290.
  8. K. Szyszkiewicz, J. J. Jasielec, M. Danielewski, A. Lewenstam, R. Filipek, “Modeling of Electrodiffusion Processes from Nano to Macro Scale”, Journal of The Electrochemical Society, 164, (2017), E3559–E3568.
  9. J.J. Jasielec, R. Filipek, K. Dołowy, A. Lewenstam, Precipitation of Inorganic Salts in Mitochondrial Matrix, Membranes, 10, (2020), 81–109.

Contact: Prof. Robert Filipek